Turunan (Diferensial) menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya.
Turunan dapat dinyatakan dalam bentuk limit.
Misal ![]() maka turunan fungsi f terhadap x dinyatan sebagai
maka turunan fungsi f terhadap x dinyatan sebagai
![]()
contoh: Tentukan turuna dari ![]() (pembahasan ada pada video)
(pembahasan ada pada video)
berdasarkan perhitungan turunan berdasarakan limit, maka dapat dibuat rumus turuna fungsi dari fungsi ![]() adalah
adalah
![]()
Sifat-sifat Turunan
Jika u dan v adalah fungsi-fungsi dalam variabel x dan c adalah konstanta, maka berlaku:
- Turunan
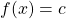 adalah
adalah 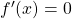 (turunan konstanta adalah 0)
(turunan konstanta adalah 0) - Turunan
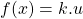 adalah
adalah 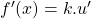
- Turunan
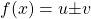 adalah
adalah 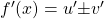
- Turunan
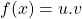 adalah
adalah 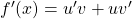
- Turunan
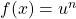 adalah
adalah 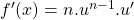
- Turunan
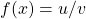 adalah
adalah 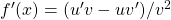
selengkapnya tentang contoh soal dari sifat-sifat turunan ada pada video berikut:
1. video hibungan turunan dan sifat 1, 2, 3, dan 5
2. Penjelasan dan contoh sifat perkalian dan pembagian.
atau
Visited 177 times, 1 visit(s) today






